Exponential Sums

Exponential sums come from the Fourier transform of some pattern. The Fourier theory of addition modulo q gives q-th roots of unity, the Fourier theory of multiplication modulo q gives Dirichlet characters. The Fourier theory of addition on the real line gives ordinary Fourier series, that of multiplication gives Dirichlet series. The Fourier theory of 2 by 2 matrices can be used to investigate equations of the form ad-bc=h, and also bulk properties of the Kloosterman sums K(m,n;q) , which are Fourier transforms of the pattern of multiplicative inverses modulo q. Weyl Sums Σe(f(m)), where e(t) means exp(2Πit), and f(m) is a polynomial, are used to investigate representations of numbers in various forms. Van der Corput sums Σe(f(m)) , where f(m) is highly differentiable but not a polynomial, are used to count the number of integer points in regions with curved boundaries like xy < N; they also appear in studies of the  Riemann zeta function.

Table of solutions of xy congruent to 1 (modulo 11)

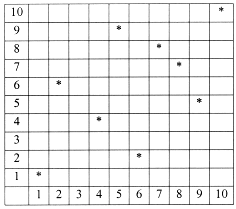
The Kloosterman sums are the finite Fourier transforms of this picture.

References

• M. N. Huxley, Integer points, exponential sums and the Riemann zeta function, Number Theory for the Millennium, Natick 2002, vol. II, 275-290.
• G. R. H. Greaves, G. Harman, M. N. Huxley (ed), Sieves, Exponential Sums, and their Applications in Number Theory, Cambridge 1997.
• M. N. Huxley, Area, Lattice Points and Exponential Sums, Oxford 1996.