Multiplicative properties of nearby integers

Is every prime number of the form n!+1 or n!-1? Can n and n+2 both be prime numbers? Can you have a long sequence of integers, none of which is a sum of two squares? These and other questions lead to equations of the form ad-bc=h, where h is small, and a, b, c, d are integers of specified types. Approaches to these questions may involve sieves or exponential sums, especially Kloosterman sums.

Table of sums of two squares:

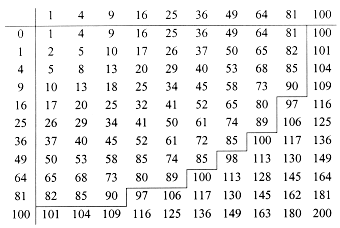
There is a gap between 90 and 97 in which no integer is a sum of two squares.

References

• G. R. H. Greaves, G. Harman, M.N. Huxley (ed.) Sieve Methods, Exponential Sums, and thir Applications in Number Theory , Cambridge 1997.