Integer points in higher dimensions

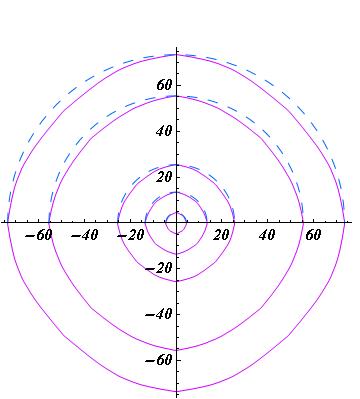
The problem of counting integer lattice points inside, on, and near convex hypersurfaces (and curves) is a classical and time-honoured problem in Number Theory and related areas. In 1925 V. Jarnik linked convex curves to convex polygons via a greedy algorithm to obtain an upper bound for the number of lattice points lying on a curve (centred Jarnik polygons’ of height 2,3,4,5 and 6 versus semi-circles of the polygon diameters are depicted below). Since then, much progress has been made with the generalised problem of counting the number of lattice points close to convex surfaces in higher dimensional space. The interplay between the “smoothness conditions” imposed on the surface and the size of the upper bound is fundamental and currently the subject of much interest. From the image below it would appear that the limiting curve of the Jarnik polygon is not circular and in fact it was proved by G. Martin that it consists piecewise of arcs of parabolas (see references).

 

References M. N. Huxley, Area, lattice points, and exponential sums, The Clarendon Press, Oxford University, 1996. A. Iosevich and K. Taylor, Lattice points close to families of surfaces, nonisotropic dilations and regularity of generalized Radon transforms, New York J. Math. 17 (2011), 811–828. V. Jarnik, Uber die Gitterpunkte auf konvexen Kurven, Math. Zeitschrift 24 (1925), 500-518. M. C. Lettington, Integer points close to convex surfaces, Acta Arith. (1) 138 (2009), 1-23. M. C. Lettington, Integer points close to convex hypersurfaces, Acta Arith. (1) 141 (2010), 73-101. G. Martin, The limiting curve of Jarnik’s polygons’, Trans. Amer. Math. Soc. (12) 355 (2003), 4565-4880.

 

Back to Number Theory home page